Reviewed by Alex SmithJul 20 2021
Researchers have developed a new mathematical model that enables even slight changes in carbon-based materials to be predicted, paving the way for exciting properties.
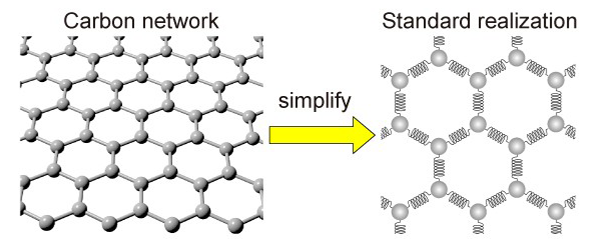The simplification of a carbon network. The carbon network can be replaced with balls and springs for simplification. Image Credit: Kotani et al.
The breakthrough was achieved by researchers from Tohoku University along with their collaborators in Japan. The mathematical model is capable of outlining the main effects of changes made to the geometries of carbon materials and predicting their special properties.
The study was published in the journal Carbon. It is common practice for researchers to employ mathematical models to forecast the characteristics that could arise when a material is subjected to change in specific ways.
For example, altering the geometry of three-dimensional (3D) graphene, which is formed by a network of carbon atoms, by chemical treatment or by introducing topological defects can help enhance its catalytic properties. However, it has been challenging for researchers to comprehend the exact cause.
The newly developed mathematical model known as Standard Realization with Repulsive Interaction (SRRI) uncovers the relationship between these variations and the properties that emerge from them. This operation is being performed with less computational power compared to the density functional theory (DFT), a typical model used for this purpose, but less precise.
The researchers have used the SRRI model to improvise another existing model by exhibiting the attractive and repulsive forces that prevail between the adjacent atoms in carbon-based materials. Moreover, the SRRI model considers two types of curvature in such materials, namely, mean curvature and local curvature.
The research group was headed by Motoko Kotani, a mathematician at Tohoku University. They employed their model to estimate the catalytic properties that would emerge while introducing local curvature and dopants into 3D graphene. The outcomes were similar to the ones obtained from the DFT model.
The accuracy of the SRRI model showed a qualitative agreement with DFT calculations, and is able to screen through potential materials roughly one billion times faster than DFT.
Motoko Kotani, Study Lead and Mathematician, Tohoku University
Then, the researchers fabricated the material and identified its characteristics with the help of scanning electrochemical cell microscopy. This technique can establish a direct link between the geometry of the material and its catalytic activity. It showed that the catalytically active sites lie on local curvatures.
Our mathematical model can be used as an effective pre-screening tool for exploring new 2D and 3D carbon materials for unique properties before applying DFT modeling. This shows the importance of mathematics in accelerating material design.
Motoko Kotani, Study Lead and Mathematician, Tohoku University
The researchers look forward to employing their model to search for links between the material’s design and its electron and mechanical transport properties.
Journal Reference:
Dechant, A., et al. (2021) Geometric model of 3D curved graphene with chemical dopants. Carbon. doi.org/10.1016/j.carbon.2021.06.004.