Depending on the defect structure, functional defects in periodic media constrain waves in multiple dimensions. While defects are represented by a superlattice with a standard band structure, representing energy levels, quantifying the confinement linked to a specific band is extremely difficult, and no analytical approach is currently available.
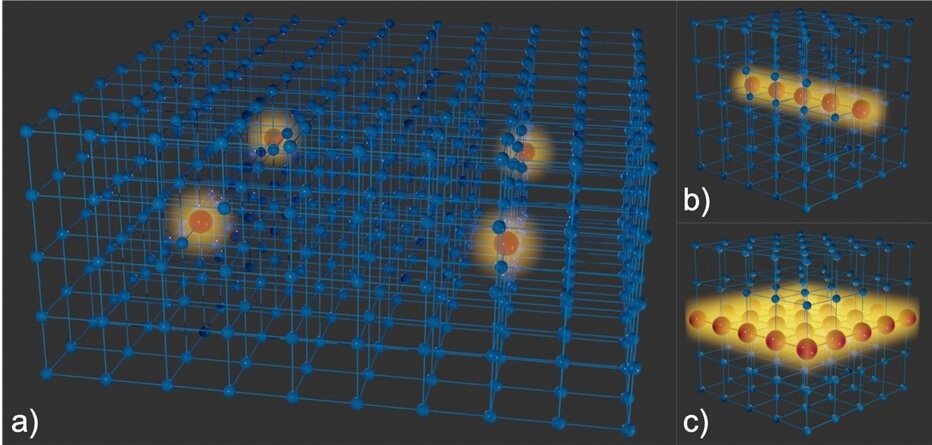
Illustration of a 3-dimensional crystal with various types of confining centres. Blue spheres represent unmodified unit cells, and red spheres are confining centres. (a) Crystal with four confining centres, each trapping waves (yellow) in all three dimensions (c=3) simultaneously. (b) Crystal with a linear confining centre where waves can propagate in 1 dimension, analogous to an optical fibre (c=2). (c) Crystal with a planar confining centre where waves can propagate in 2 dimensions, analogous to a 2D electron gas (c=1). Image Credit: University of Twente
An article published in Physical Review Letters proposed a robust approach for classifying wave confinement dimensionality. Starting from the mode volume and the confinement energy, the finite-size scaling was employed to discover that ratios of these values raised to specific powers revealed the confinement dimensionality of each band.
Compared to the calculations of band structure, the classification proposed in this work required no computational costs and was valid for both classical and quantum waves in all dimensions. The present approach for electronic confinement was demonstrated in two-dimensional (2D) hexagonal boron nitride (hBN) with a nitrogen vacancy in the quantum regime, which agreed with previous results.
Additionally, a three-dimensional (3D) photonic band gap cavity superlattice was studied, which revealed a unique acceptor-like behavior.
Applications of Wave Confinement
Complete control of wave transport is challenging and critical for a broad range of applications. For example, the classical transport of acoustic waves has enabled sensing, ultrasound imaging, and navigation.
Control over the spin and electron transport in the quantum regime has resulted in significant breakthroughs in the operation of nanoelectronic devices. Controlling light transmission in the classical and quantum domains in photonics has resulted in substantial technological advancements in solar cells, quantum light sources, optical memory, and microscale to nanoscale storage cavities.
Wave confinement by introducing functional defects or disorders into periodic media is an intriguing method to control wave propagation. Such altered structure-wave interference may induce a strong energy concentration inside a small volume of the medium.
Analyzing a physical system’s spatial concentration of energy is traditionally possible via mode volume in photonics and participation ratio in condensed matter physics. Bands with a small participation ratio or mode volume were confined, and those with a large participation ratio or mode volume were considered extended. Moreover, since there are no stringent boundaries imposed naturally, the notion of “small” and “large” is subjective.
Alternatively, the wave confinement can be determined based on a multifractality analysis that relies on the participation ratio measurement within an infinitely large supercell. However, this approach requires inconceivable large supercells, which are reinforced by their inability to handle band folding.
2D hBN is an isomorph of graphene with a very similar layered structure, which is uniquely characterized by its exotic optoelectrical properties, mechanical robustness, thermal stability, and chemical inertness.
hBN is naturally covalent, and the electrons in the sigma bond are localized towards nitrogen, whereas the pi bonding present involves an empty p-orbital of boron and a filled p-orbital of nitrogen, with the nitrogen pi electrons delocalized.
Scaling Theory of Wave Confinement
The present work demonstrated a rigorous method to determine wave confinement in defects containing periodic structures. This method is based on finite-size scaling, which determines the wave confinement in moderately large supercells instead of extending them to impractically large sizes.
Consequently, the current method has a relatively low computational cost, and its findings can be applied to practically relevant confined systems. This approach is a practical and accessible extension of the multifractality concept and is suitable for automatic classification.
The scaling theory of wave confinement was determined using 2D hBN, with nitrogen vacancies representing point-like defects. Here, electronic confinement was investigated in a supercell size (N) of 5. Density functional theory (DFT) calculations were performed to determine charge densities and band structures.
Previous researchers have mentioned that in structures with higher dimensions, there is no direct correlation between coupling and dispersion in any given direction, making it challenging to assess confinement by analyzing band dispersion.
However, the present method enabled the determination of wave confinement in high-dimensional structures, demonstrated by utilizing a 3D inverse woodpile photonic crystal with two proximate line defects, which otherwise failed the dispersion arguments in the literature.
Furthermore, this method was not constrained to impurities or defects containing superlattices but was also applied to analyze any superlattice superimposed on another lattice, which is relevant to flat-band and Lieb lattices.
Conclusion
In summary, a systematic scaling theory was proposed in this work for analyzing the wave confinement of a periodic superlattice which is relevant to any form of a physical wave. The negligible computational cost is more advantageous than the precedented complex band structure calculation.
This approach is directly applicable to currently investigated quasiperiodic and periodic structures and optimization algorithms aimed at minimizing or maximizing certain forms of wave confinement.
Reference
Kozoň, M., Lagendijk, A., Schlottbom, M., van der Vegt, J. J., Vos, W. L. (2022). Scaling theory of wave confinement in classical and quantum periodic systems. Physical Review Letters. https://link.aps.org/doi/10.1103/PhysRevLett.129.176401
Disclaimer: The views expressed here are those of the author expressed in their private capacity and do not necessarily represent the views of AZoM.com Limited T/A AZoNetwork the owner and operator of this website. This disclaimer forms part of the Terms and conditions of use of this website.