Jul 9 2009
Let's assume we carried out the following experiment: we put a coin in the hand of a test person. We’ll simply call this person Hans. Hans's task is now to toss the coin several times. Whenever the coin turns up 'heads', his task is to take a step to the right. By contrast, if it turns up 'tails', he takes a step to the left. After 10 throws we look where Hans is standing. Probably he won't have moved too far from his initial position, as 'heads' and 'tails' turn up more or less equally often. In order to walk 10 paces to the right, Hans would have to get 10 'heads' successively. And that tends not happen that often.
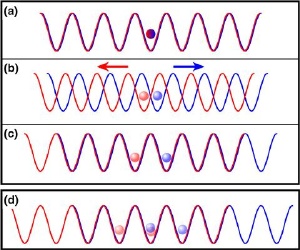a) A single caesium atom is trapped in grid of light. The atom has two states, red and blue. b) The light grid is dependent on the state of the atom. It can be visualised as a red and a blue grid where the red state of the atom only sees the red grid and the blue state of the atom only sees the blue grid. c) If both subgrids overlap again, the atom is spread over two grid sites, i.e. it is simultaneously located at the right and left. d) After each part of the atom has again been brought into a superposition of both states and the state-dependent shift has been carried out, the atom is delocalised over three grid sites, where two parts of the atom are now situated in the same grid site.
Now, we assume that Hans is a very patient person. He is so patient that he does this experiment 1000 times successively. After each go, we record his position. When at the end we display this result as a graph, we get a typical bell curve. Hans very often ends up somewhere close to his starting positions after 10 throws. By contrast, we seldom find him far to the left or right.
The experiment is called a 'random walk'. The phenomenon can be found in many areas of modern science, e.g. as Brownian motion. In the world of quantum physics, there is an analogy with intriguing new properties, the 'quantum walk'. Up to now, this was a more or less a theoretical construct, but physicists at the University of Bonn have now actually carried out this kind of 'quantum walk'.
A single caesium atom held in a kind of tweezers composed of laser beams served as a random walker and coin at the same time. Atoms can adopt different quantum mechanical states, similar to head and tails of a coin facing upwards. Yet at the microcosmic level everything is a little more complicated. This is because quantum particles can exist in a superposition of different states. Basically, in that case 'a bit of heads' and 'a bit of tails' are facing upwards. Physicists also call this superposition.
Using two conveyor belts made of laser beams, the Bonn physicists pulled their caesium atom in two opposite directions, the 'heads' part to the right, the 'tails' part to the left. 'This way we were able to move both states apart by fractions of a thousandth of a millimetre,' Dr. Artur Widera from the Bonn Institute of Applied Physics explains. After that, the scientists 'threw the dice once more' and put each of both components into a superposition of heads and tails again.
After several steps of this 'quantum walk' a caesium atom like this that has been stretched apart is basically everywhere. Only when you measure its position does it 'decide' at which position of the 'catwalk' it wants to turn up. The probability of its position is predominantly determined by a second effect of quantum mechanics. This is due to two parts of the atom being able to reinforce themselves or annihilate themselves. As in the case of light physicists call this interference.
As in the example of Hans the coin thrower, you can now carry out this 'quantum walk' many times. You then also get a curve which reflects the atom’s probability of presence. And that is precisely what the physicists from Bonn measured. 'Our curve is clearly different from the results obtained in classical random walks. It does not have its maximum at the centre, but at the edges,' Artur Widera's colleague Michal Karski points out. 'This is exactly what we expect from theoretical considerations and what makes the quantum walk so attractive for applications.' For comparison the scientists destroyed the quantum mechanical superposition after every single 'throw of the coin'. Then the 'quantum walk' becomes a 'random walk', and the caesium atom behaves like Hans. 'And that is exactly the effect we see,' Michal Karski says.
Professor Dieter Meschede's group has been working on the development of so-called quantum computers now for many years. With the 'quantum walk' the team has now achieved a further seminal step on this path. 'With the effect we have demonstrated, entirely new algorithms can be implemented,' Artur Widera explains. Search processes are one example. Today, if you want to trace a single one in a row of zeros, you have to check all the digits individually. The time taken therefore increases linearly with the number of digits. By contrast, using the 'quantum walk' algorithm the random walker can search in many different places simultaneously. The search for the proverbial needle in a haystack would thus be greatly speeded up.