Electron Self-Injection and Acceleration in an Expanding Plasma Bubble

Particle accelerators are among the largest and most expensive scientific instruments. Thirty years ago, theorists John Dawson and Toshiki Tajima proposed an idea for making them thousands of times smaller: surf the particles on plasma waves driven by short intense laser pulses. Since plasmas are free of the damage limits of conventional accelerators, much larger fields can be built up within such waves, enabling much smaller accelerators.

Just five years ago, experimentalists finally demonstrated that such laser-plasma accelerators could produce monoenergetic, collimated electron beams with quality comparable to conventional accelerators. The secret was for the laser to produce a "bubble" almost completely devoid of electrons in its immediate wake that captured electrons from the surrounding plasma and accelerated them in an exceptionally uniform way. Yet the precise mechanism by which the bubble captured these electrons and accelerated them with such uniformity has remained one of the outstanding mysteries of this field.

Now new theoretical work by scientists from the University of Texas and Commissariat à l'Énergie Atomique (CEA, France), to be reported at the 2009 APS Division of Plasma Physics Annual Meeting, has shed light on this mystery. Formation of the exceptional quality electron beam is attributed to the evolution of the bubble shape which, in turn, is directly associated with the nonlinear evolution of the driving laser pulse (nonlinear focusing and defocusing).

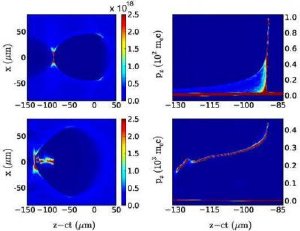
The basic premise of this work is that the size of the bubble—the cavity of electron density traveling over the positive ion background with nearly the speed of light—is determined by the spot size of the driving laser pulse. Plasma nonlinearities cause the laser to focus and defocus in the course of propagation. Once the laser diffracts, the bubble expands. Electrons that constitute a dense electron shell surrounding the bubble move with relativistic speeds and thus have high inertia. As a consequence, some of them become too heavy to follow the expanding shell; they fall inside the bubble, stay inside till the end of the plasma (i.e. get trapped) and finally gain multi-GeV energy. The trapped charge is proportional to the bubble growth rate. Once the laser becomes self-guided, and the spot size oscillations saturate, the injection process clamps. Simultaneously, longitudinal non-uniformity of the accelerating gradient equalizes the trapped electron energy. This scenario of self-injection and monoenergetic bunch formation is discovered and explored in fine detail in the 3-D particle-in-cell simulations. This is fundamentally different from the previous work which concentrated on either one-dimensional models of electron trapping or on the reduced description of transverse plasma wave breaking in planar 2-D geometry.

The discussed mechanism of electron self-injection is very robust in experiments with the high-power laser (tens of terawatts to petawatt). In addition, an appropriate modification of the plasma density (e.g. using a thin dense slab as a nonlinear lens for the laser) may cause the laser to self-focus and defocus faster, which results in a single self-injection event. This kind of laser beam manipulation may lead to the generation of a 2.5 GeV mono-energetic (~1% energy spread) electron bunch containing ~1010 electrons in a future experiment with the recently commissioned Texas Petawatt (TPW) laser – the most powerful laser in the world. Electrons with 2.5 GeV of energy are traveling at 99.999998% of the speed of light. Electron beams with such unique properties are clearly beneficial for medical applications, radiation physics, material science, and homeland security (see, e.g., talks TO4.00004 and TO4.00005, this Meeting).